Struktury zagrodenów oferują inne ciekawe możliwości do zbadania. Przede wszystkim zależało mi, żeby się dowiedzieć, czy modele poszerzone o jedną warstwę dają stabilne geometrie. W tym celu skonstruowałem układy geometryczne zawierające 3, 4, 5, 6 oraz 9 łańcuchów homoallenowych w każdej warstwie (czyli w dwu warstwach ogółem). Podobnie jak poprzednio przyjąłem, że modele te będą miały oznaczenia zagrodenx-3, gdzie x jest liczbą łańcuchów homoallenowych w warstwie, natomiast 3 oznacza liczbę dwóch skrzydłowych pierścieni połączonych grupami metylenowymi plus jeden pierścień środkowy.
Analizę struktur rozpocząłem od zagrodenu3-3. Optymalizację wykonałem na poziomie HF/6-31G(d)/hess-plus (a także na poziomie DFt – B3LYP/def2-SVP/hess-plus). Poniżej zamieszczony jest aktywny model 3D zagrodenu3-3:
Mała średnica w tej strukturze wywołuje naprężenie objawiające się zagięciem układu homoallenowego. To naprężenie jest mniejsze w następnym modelu zagrodenu4-3 [HF/6-31G(d)/hess-plus] ale także na poziomie DFT (Orca.4.2.1/B3LYP/def2-SVP/hess-plus):
Można tu wyróżnić dwa kąty walencyjnie w łańcuchu homoallenowym wynoszące 157.4° oraz 160.9° są to kąty odpowiednio dla trzech wewnętrznych i trzech zewnętrznych atomów węgla łańcuchów homoallenowych.
Poniżej znajdują się obrazy zagrodenu5-3 oraz 6-3 (obrazy wygenerowane przez Avogadro 1.98.1):
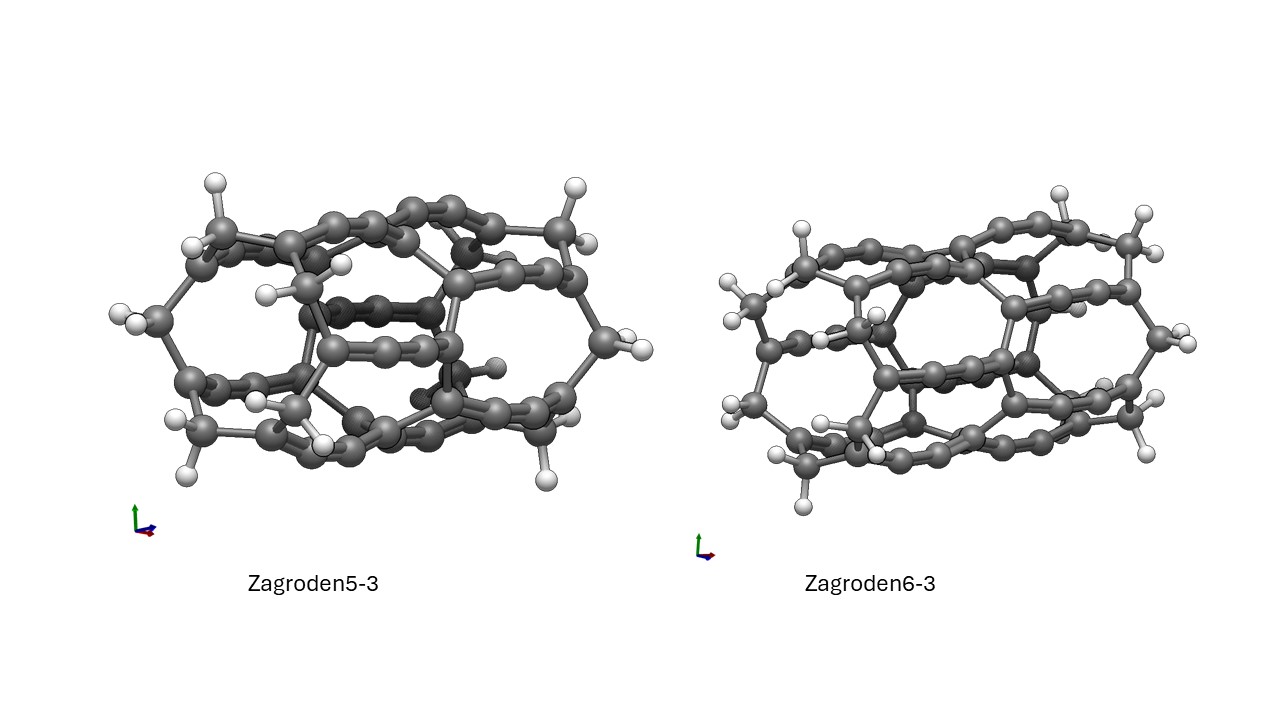
Obliczenia dla powyższych struktur zostały wykonane na poziomie HF/6-31G(d)/hess-plus. Nie badałem struktur zagrodenów7-3 oraz 8-3. Natomiast przedmiotem badań był zagroden9-3. Obliczenia za pomocą programu Orca4.2.1 na poziomie HF/6-31G(d) wykazały obecność czterech ujemnych częstości (film – program Avogadro 1.98.1 jest poniżej):
Zachowanie się drgań ujemnych sugeruje, że droga do ich likwidacji powinna polegać, jak sądzę, na przegięciu niektórych łańcuchów homoallenowych do wnętrza cząsteczki. Zagadnienie to jest jednak w czasie publikacji tego wpisu (styczeń 2024) nadal otwarte.