Następny model różni się do poprzednich tym, że zmostkowane zostały atomy węgla leżące na zewnątrz makrocyklu. Zauważyłem, że ułożenie atomów wodotu może sprzyjać ich podstawieniu przez fragmenty allenowe -C=C=CH-. Ten zabieg konstrukcyjny dał cząsteczkę, która uległa optymalizacji i relaksacji na poziomie PM3 (Orca 4.2.1/ PM3/ hess-plus):
Tę serię zakończył model z wstawionymi atomami azotu (parametry obliczeń jak wyżej):
Nową serię związków rozpocząłem od usztywnienia modelu A z poprzedniej strony. Atomy wodoru pierścieni ekwatorianych względem płaszczyzny makrocyklu podstawiłem grupami metylenowymi. Zrobiłem to w taki sposób, że grupy -CH2– połączyły sąsiednie atomy węgla fragmentów etenowych. W ten sposób powstał model A1 (rysunek poniżej – dobudowane atomy węgla zaznaczyłem kolorem czerwonym, atomy wodoru usunięte dla klarowności rysunku):
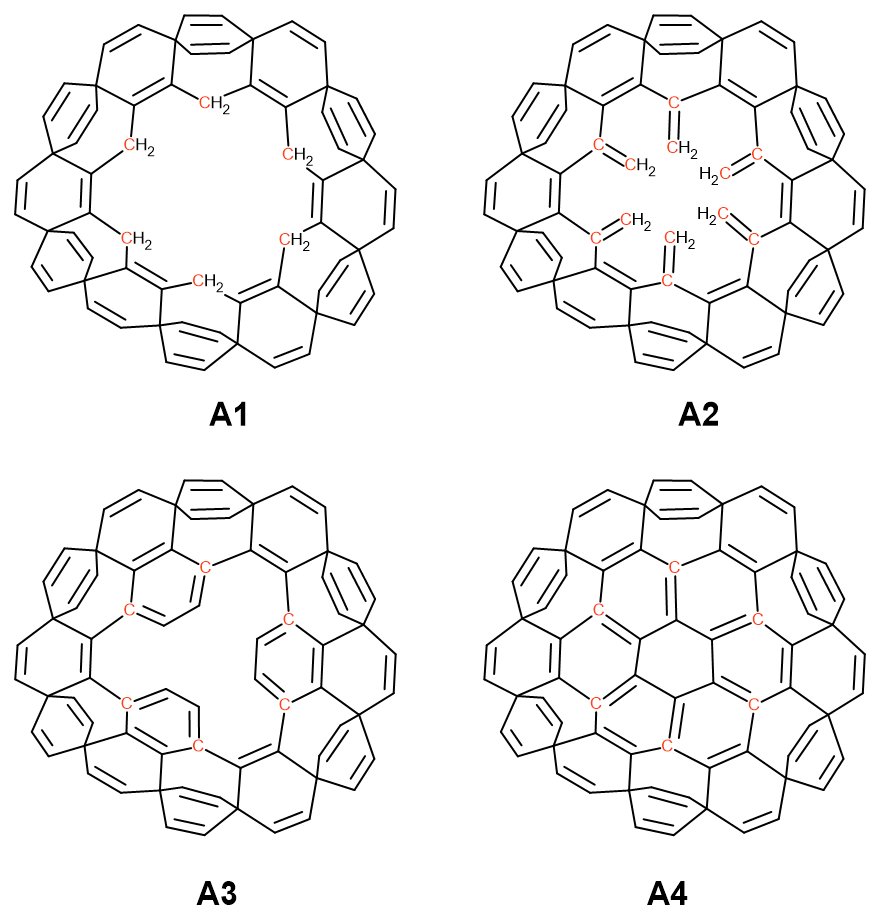
W etapie drugim dobudowałem grupy CH2 w sposób pokazany na modelu A2 (rysunek powyżej). Pary tych grup połączyłem wiązaniem pojedynczym (A3). Wreszcie utworzyłem wewnętrzny pierścień sześcioczłonowy (A4). Modele A1–A3 optymalizowałem jedynie za pomocą modułu MM w programie ChemSketch. Dopiero model A4 poddałem procesowi optymalizacji na poziomie półempirycznym. Okazało się, że optymalizacja udawała się gładko, ale relaksacja nie powiodła się zarówno dla metody PM3 (Orca 4.2.1) jak i PM7 (MOPAC 22.1.1). Obecna była jedna częstość ujemna o małej wartości 4.38 cm-1. Charakter tego „drgania” był na tyle skomplikowany, że to skomplikowanie nie pozwalało mi na odkrycie metody zrelaksowana cząsteczki poprzez ręczne przesunięcia wybranych atomów. Rozwiązanie przyszło z innej strony.
Zanim znalazłem to rozwiązanie, skonstruowałem cząsteczkę nowego związku skondensowaną z dwóch płatów modelu A4. Konstrukcja składała się z jednego płatu A4 pozbawionego aksjalnych grup -CH=CH- i drugiego A4 skondensowanego z pierwszym za pomocą pojedynczych wiązań C-C takiego samego fragmentu, czyli -CH=CH-, ale wiązania te zostały utworzone w miejscach atomów wodoru (Orca 4.2.1/ PM3/ hess-plus):
Dodatkowo zauważyłem, że łączenie to można zbudować w izomeryczny sposób. Wykonałem nowe połączenie przekręcając oba płaty względem siebie o 30° (parametry obliczeń jak wyżej):
Pomyślałem, że jeśli oba izomery dają się skutecznie zrelaksować, to może ich geometria będzie właściwym stanem wyjściowym do optymalizacji i relaksacji A4. W rym celu rozdzieliłem oba płaty. Fragment z grupami -CH=CH- odtworzyłem przez ostrożne dorysowanie atomów wodoru do atomów węgla. Uzyskaną strukturę wyjściową poddałem optymalizacji. Rzeczywiście uzyskana optymalna struktura okazała się również zrelaksowana (parametry obliczeń jak wyżej):
Jak widać na powyższej ręcznej animacji, cząsteczka nie jest płaska, ale ma raczej kształt siodła.
Cyklosy3 – klik