Z czystej ciekawości postanowiłem zoptymalizować jeszcze geometrie sześciu tripanenów. W kolejności zawierających: 4-3-3, 4-4-3, 4-4-4, 5-4-4 oraz 6-5-4 nienasyconych łańcuchów węglowych połączonych z dwoma atomami azotu. Pierwszym był (2Z,7M,10M)-1,6-diazabicyklo[4.3.3]dodeka-2,3,4,7,8,10,11-heptaen (parametry obliczeń jak wyżej):

W nazwie tego związku zaskakujące jest pojawienie się deskryptora 2Z (nazwa związku została wygenerowana w programie ChemSketch 2023). Litera ta stosowana jest do opisu konfiguracji przy atomach połączonych wiązaniem podwójnym. Jest tu wiązanie podwójne, ale w układzie sprzężonym. Zdaje się, że określenie tej konfiguracji jest zgodne z regułami CIP o ile zachowa się położenia (E,Z) kolejnych atomów względem wiązania podwójnego. To by się zgadzało.

Sytuacja nazewnicza powtarza się w wypadku następnego modelu. Chodzi o (2Z,7Z,11M)-1,6-diazabicyklo[4.4.3]trideka-2,3,4,7,8,9,11,12-octaen (parametry obliczeń jak wyżej):

Kolejny związek zawiera trzy jednakowe łańcuchy butatrienowe, co powinno usunąć źródło chiralności znajdujące się w łańcuchu allenowym (parametry obliczeń jak wyżej):

Nazwa wyżej pokazanego związku to: (2Z,7Z,11Z)-1,6-diazabicyklo[4.4.4]tetradeka-2,3,4,7,8,9,11,12,13-nonaen (parametry obliczeń jak dla pierwszej struktury):

Rzeczywiście łańcuchy czterowęglowe nie generują chiralności osiowej. Cząsteczka pokazana powyżej wydaje się być więc achiralna.

Sprawę chiralności postanowiłem sprawdzić na cząsteczce, w której jeden łańcuch czterowęglowy został rozbudowany o jeden atom węgla. Powstała cząsteczka (2M,8Z,12Z)-1,7-diazabicyklo[5.4.4]pentadeka-2,3,4,5,8,9,10,12,13,14-dekaenu jest chiralna i wykazuje tu konfigurację typu M (znowu minus – parametry obliczeń jak wyżej):

Odnoszę wrażenie, przypatrując się uważnie strukturze pokazanej powyżej, że również łańcuchy parzystowęglowe są nieco skręcone. Oba mają konfigurację M, choć to skręcenie to jest niewielkie. Tym niemniej, kąty dwuścienne (torsyjne) wskazane na poniższym obrazku a zbudowane na łańcuchach czterowęglowych nie są zerowe (wizualizacja program jmol z danych s pliku typu sdf wygenerowanego przez program Avogadro 1.99 na podstawie wyników obliczeń z programu Orca 4.2.1):

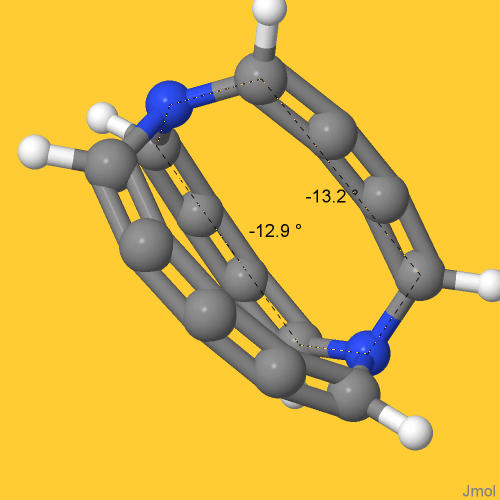
Ten rezultat może sugerować, że i one wnoszą swój wkład do całkowitej chiralności cząsteczki. Dodam, że analogiczny kąt dwuścienny zbudowany na łańcuchu pięciowęglowym jest znacznie większy i wynosi około -33.1°.

Ostatnią cząsteczką, którą zbudowałem w tej serii jest (9P,14Z)-1,8-diazabicyklo[6.5.4]heptadeka-2,3,4,5,6,9,10,11,12,14,15,16-dodekaen. Starałem się odwrócić typową dla mojej pracy manualnej konfigurację. Tym razem źródłem chiralności jest fragment pięciowęglowy, który ma konfigurację (P). Również pozostałe łańcuchy wnoszą niewielki wkład (P) do całkowitej konfiguracji cząsteczki (parametry obliczeń jak wyżej):